比较排序

对于任意的比较排序算法，我们都能将其操作抽象成一颗决策树，这是一颗完全二叉树，它表示了某一排序算法对所有元素的比较操作。下图是插入排序的例子：

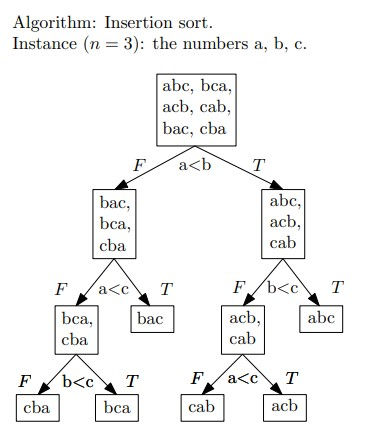
每一条路径都是一种可能性，所以算法的最坏情况下的排序次数就是决策树的高度。

n个元素，可能的排序结果有A(n,n-1)=n!种，假设此时的树高为h，则叶子节点最多为2^(h+1)

2^(h+1) ≥ n!  
h + 1 ≥ log2(n!)

而 log(n!) = O(nlogn)。

证明：

不等式缩放

log(n!) = log1 + ... + logn ≥ n/2 * log(n/2) = n/2 * logn - n/2 = c1 * logn
log(n!) = log1 + ... + logn ≤ nlogn = c2 * logn

Stirling 近似

计数排序

计数排序的思想是：在待排序序列中，如果我们能统计出有多少元素小于或等于某一个元素，我们也就知道了该元素的正确位置。 计数排序本质上是一种特殊的桶排序，当桶的个数最大的时候，就是计数排序。 例如：有五个元素小于x，那么就把x放到第六位（对于相同的元素我们认为最早遇到小于后面遇到的）。

实现该算法我们需要三个数组，初始input，结果output和表示元素统计数的count数组。 下面为算法的伪代码：

count = array of k+1 zeros
for x in input:
   count[key(x)] += 1

total = 0
for i in 0, 1, ... k:
   count[i], total = total, count[i] + total

output = array of the same length as input
for x in input:
   output[count[key(x)]] = x
   count[key(x)] += 1

return output

算法可视化

时间复杂度分析：假设在[0,k]的n个元素，数组初始化O(k)，构造统计数组C是O(n)，统计数累加O(k)，排序是O(n) 所以总共时间复杂度为O(k+n)，所以计数排序的使用场景通常是区间端点比较接近时，复杂度较低。 对于区间较大，而待排序数据分布比较均匀时，可以考虑桶排序。

计数排序是一种典型空间换时间的算法。

性能比较

下面是JS中的性能对比：

Array with 10000000 elements:
n log(n) takes 15.611 seconds
Linear takes 3.896 seconds

参考文章： https://medium.com/free-code-camp/my-favorite-linear-time-sorting-algorithm-f82f88b5daa1