考虑一个问题,平均在多少人中才能找到一对相同生日?
答案是23人。
换一个角度,如果你进入了一个有着23个人的房间,房间里的人中会和你有相同生日的概率便不是50:50了,而是变得非常低。原因是这时候只能产生23种不同的搭配。根据下面概率公式,只有n=253时,能让某人生日与我相同的概率为1/2。 $\begin{aligned} y=(1-\frac{1}{365})^n\end{aligned}$
生日问题实际上是在问任何23个人中会有两人生日相同的概率是多少,也就是说没有特定人选。 $\begin {aligned} y=1-\dfrac {365!}{365^{n}\left( 365-n\right) !}\end{aligned}$
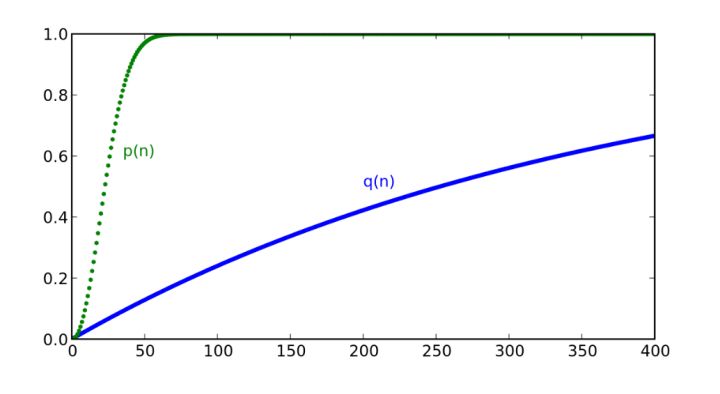
比较这两者曲线,第二种的增长非常快:
#include<stdio.h>
int main()
{
int T,n,i;
scanf("%d",&T);
int k=0;
while(T--)
{
scanf("%d",&n);
double p=1.0;
int num=0;
for(i=0;; i++)
{
p=p*(1-(double)i/n);
num++;
if(1.0-p>=0.5)
break;
}
printf("Case %d: %d\n",++k,num-1);
}
return 0;
}
应用
Pollard’s Rho整数因子分解算法
假设 ? 是一个能被分解为 ? ∗ ? 的数 ( ? = ? ∗ ? 且 ? ≠ ? ) 我们的目标是找到 ? 的其中一个因子 ? 或 ? (另外一个因子可以通过除 ? 来得到 )
最传统的方法是试除法
let N = 29;
let flag = 1;
if(N % 2 == 0) flag = 0; //首先测试 N 是否是偶数
else for(let i = 3;i * i < N;i += 2){ //与刚才不同的是,我们先从 3 开始,每次增加 2,一直
//到根号下 N 为止。这样我们的测试就在奇数中展开
if(N % i == 0){
flag = 0;
break;
}
}
我们随即地从[1,N]中选择一个数,这个数是 p 或者 q 的可能性是非常小。但是我们可以转换角度,不再只选取一个整数,我们能够选取 k 个数,然后在这k个数中寻找是否存在a − b 能够整除 ?。这样我们就将概率从我们可以将可能性从 1/? 提高到√1/?。
做差之后等于p或q,只有两个还是太少了,我们可以还可以更进一利用最大公约数gcd(|a - b| ,N) > 1,满足这个条件的就多了?,2?,3?,4?,……,(? − 1)?,?,2?,3?,4?,……,(? − 1)?一共有? + ? − 2 个数,到现在我们只需要大约 $N^(1/4) $ 个数。
在实际计算时,我们不预先生成随机数,而是一个一个地生成并检查连续的两个数。
// 随机数生成
function g (x, prime) {
return (Math.pow(x, 2) + 1) % prime
}
// 最大公约数
function gcd (a, b) {
if (!b) return a;
return gcd(b, a % b)
}
function pollardRho (prime) {
let x = 2;
let y = 2;
let d = 1;
while (d === 1) {
x = g(x, prime); //x runs once
y = g(g(y, prime), prime); ; //y runs twice as fast
d = gcd(Math.abs(x - y), prime);
if (d === prime) return;
if (d !== 1 && !isNaN(d)) return d;
}
}
哈希碰撞
我们以CRC16 为例,哈希值是17位,2 ^ 8 = 256 个项目的集合中,哈希冲突的机率就会达到约为50%。 这里是CRC16-CRC64的测试 1
安全的Hash标准的输出长度选为160比特是出于这种考虑。
参考文章
http://www.math.umbc.edu/~campbell/NumbThy/Class/Programming/JavaScript/ https://www.cs.colorado.edu/~srirams/courses/csci2824-spr14/pollardsRho.html https://wenku.baidu.com/view/c3e3657b27284b73f24250d5.html