优先队列（Priority Queue）

简单介绍下优先队列，它不记录入队顺序，而是当前最大/最小的元素优先出队。我们可以用最大/最小堆来实现优先队列，每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点。这篇文章以Heapify的源码为例，简要介绍其实现。

优先队列的表示

我们用数组来表示二叉堆，并将根节点的索引置为 1。Heapify 中使用使用两个独立的类型数组（默认使用 Uint32Array ）表示二叉堆。

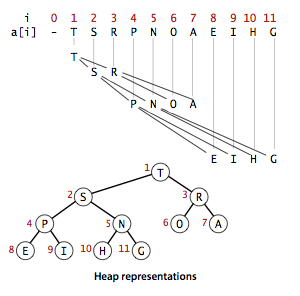
在堆中，位置k的节点的父节点在位置k / 2；相反，位于位置k的节点的两个子节点位于位置2k和2k +1。我们可以通过对数组索引执行简单的计算来上下移动。

    constructor(capacity = 64, keys = [], priorities = [],
        KeysBackingArrayType = Uint32Array,
        PrioritiesBackingArrayType = Uint32Array) {

        this.capacity = capacity;
        this._keys = new KeysBackingArrayType(capacity + ROOT_INDEX); // ROOT_INDEX = 1;
        this._priorities = new PrioritiesBackingArrayType(capacity + ROOT_INDEX);
        if (keys.length !== priorities.length) {
            throw new Error("Number of keys does not match number of priorities provided.");
        }
        if (capacity < keys.length) {
            throw new Error("Capacity less than number of provided keys.");
        }
        // copy data from user
        for (let i = 0; i < keys.length; i++) {
            this._keys[i + ROOT_INDEX] = keys[i];
            this._priorities[i + ROOT_INDEX] = priorities[i];
        }
        this.length = keys.length;
        for (let i = keys.length >>> 1; i >= ROOT_INDEX; i--) {
            this.bubbleDown(i);
        }
    }

插入或删除元素

插入或删除后都后需要重新调整堆的结构。插入时我们直接放在最后然后递归向上浮动到合适位置；删除时顶部空缺，我们先将最后一个节点换到顶部，然后将其下沉到合适位置。浮动的时间复杂度为O(log n)。

上浮

  bubbleUp(index) {
        const key = this._keys[index];
        const priority = this._priorities[index];

        while (index > ROOT_INDEX) {
            const parentIndex = index >>> 1;   // 父元素索引
            if (this._priorities[parentIndex] <= priority) {
                break;  // 如果父元素优先级更小，则满足了堆的性质
            }
            // 否则将父元素沉下来
            this._keys[index] = this._keys[parentIndex];
            this._priorities[index] = this._priorities[parentIndex];

            index = parentIndex; // 重复下一级
        }

        // 至此找到了插入元素要放置的位置
        this._keys[index] = key;
        this._priorities[index] = priority;
    }

下沉

bubbleDown(index) {
        const key = this._keys[index];
        const priority = this._priorities[index];

        const halfLength = ROOT_INDEX + (this.length >>> 1);  // no need to check the last level
        const lastIndex = this.length + ROOT_INDEX;
        while (index < halfLength) {
            const left = index << 1;
            if (left >= lastIndex) {
                break;  // 到最后一个节点，无法继续下沉
            }

            // 选择左孩子
            let childPriority = this._priorities[left];
            let childKey = this._keys[left];
            let childIndex = left;

            // 如有右孩子，选择优先级最小的
            const right = left + 1;
            if (right < lastIndex) {
                const rightPriority = this._priorities[right];
                if (rightPriority < childPriority) {
                    childPriority = rightPriority;
                    childKey = this._keys[right];
                    childIndex = right;
                }
            }

            if (childPriority >= priority) {
                break;  // 如果孩子优先级更小，则满足了堆的性质
            }

            // 否则将子元素浮上去
            this._keys[index] = childKey;
            this._priorities[index] = childPriority;

            index = childIndex;
        }

        // 至此找到了插入元素要放置的位置
        this._keys[index] = key;
        this._priorities[index] = priority;
    }

在最后实现了下面三个生成器函数，让我们可以方便的获取优先队列中的值和优先级。

   * [Symbol.iterator]() {
        for (let i = 0; i < this.length; i++) {
            const priority = this._priorities[i + ROOT_INDEX];
            const key = this._keys[i + ROOT_INDEX];
            yield [key, priority];
        }
    }

    * keys() {
        for (let i = 0; i < this.length; i++) {
            yield this._keys[i + ROOT_INDEX];
        }
    }

    * priorities() {
        for (let i = 0; i < this.length; i++) {
            yield this._priorities[i + ROOT_INDEX];
        }
    }

参考文章

https://github.com/luciopaiva/heapify/blob/master/heapify.mjs https://algs4.cs.princeton.edu/24pq/